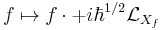Geometric quantization

In mathematical physics, geometric quantization is a mathematical approach to defining a quantum theory corresponding to a given classical theory. It attempts to carry out quantization, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory and the quantum theory remain manifest. For example, the similarity between the Heisenberg equation in the Heisenberg picture of quantum mechanics and the Hamilton equation in classical physics should be built in.

One of the earliest attempts at a natural quantization was Weyl quantization, proposed by Hermann Weyl in 1927. Here, an attempt is made to associate a quantum-mechanical observable (a self-adjoint operator on a Hilbert space) with a real-valued function on classical phase space. Here, the position and momentum are reinterpreted as the generators of the Heisenberg group, and the Hilbert space appears as a group representation of the Heisenberg group. In 1946, H. J. Groenewold (H.J. Groenewold, "On the Principles of elementary quantum mechanics", Physica,12 (1946) pp. 405-460) considered the product of a pair of such observables and asked what the corresponding function would be on the classical phase space. This led him to define the phase-space star-product of a pair of functions. More generally, this technique leads to deformation quantization, where the ∗-product is taken to be a deformation of the algebra of functions on a symplectic manifold or Poisson manifold. However, as a natural quantization scheme, Weyl's map is not satisfactory. For example, the Weyl map of the classical angular-momentum-squared is not just the quantum angular momentum squared operator, but it further contains a constant term 3ħ²/2. This extra term is actually physically significant, since it accounts for the nonvanishing angular momentum of the ground-state Bohr orbit in the hydrogen atom.

The geometric quantization procedure falls into the following three steps: prequantization, polarization, and metaplectic correction.

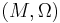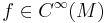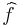Prequantization of a symplectic manifold $(M,\Omega)$ provides a representation of elements $f\in C^\infty(M)$ of the Poisson algebra of smooth real functions on $M$ by first order differential operators $\widehat f$ on sections of a complex line bundle 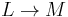$L\to M$ . 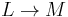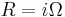In accordance with the Kostant - Souriau prequantization formula, these operators are expressed via a connection on $L\to M$ whose curvature form $R$ obeys the prequantization condition $R=i\Omega$ .
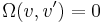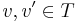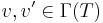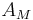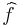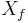By polarization is meant an integrable maximal distribution $T$ on $M$ such that $\Omega(v,v')=0$ for all $v,v'\in T$ . Integrable means $[v,v']\in\Gamma(T)$ for $v,v'\in\Gamma(T)$ (sections of T). The quantum algebra $A_M$ of a symplectic manifold $M$ consists of the operators $\widehat f$ of functions $f$ whose Hamiltonian vector fields $X_f$ satisfiy the condition $[X_f,T]\subset T$ .
In accordance with the metaplectic correction, elements of the quantum algebra 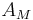$A_M$ act in the pre-Hilbert space of half-forms with values in the prequantization Line bundle on a symplectic manifold $M$ . The quantization is simply

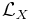$f\mapsto f\cdot %2Bi\hbar^{1/2}\mathcal{L}_{X_f}$

where $\mathcal{L}_X$ is the Lie derivative of a half-form with respect to a vector field X.

Geometric quantization of Poisson manifolds and symplectic foliations also is developed. For instance, this is the case of partially integrable and superintegrable Hamiltonian systems and non-autonomous mechanics.

References

J. Śniatycki (1980). Geometric Quantization and Quantum Mechanics. Springer. ISBN 0-387-90496-7.

N.M.J. Woodhouse (1991). Geometric Quantization. Clarendon Press. ISBN 0-19-853673-9.

I. Vaisman (1991). Lectures on the Geometry of Poisson Manifolds. Birkhauser. ISBN 978-3-7643-5016-1.

G. Giachetta, L. Mangiarotti, G. Sardanashvily (2005). Geometric and Algebraic Topological Methods in Quantum Mechanics. World Scientific. ISBN 981-256-129-3.

K.Kong Wan (2006). From Micro to Macro Quantum Systems, (A Unified Formalism with Superselection Rules and Its Applications). World Scientific. ISBN 978-1-86094-625-7.

External links

William Ritter's review of Geometric Quantization presents a general framework for all problems in physics and fits geometric quantization into this framework
John Baez's review of Geometric Quantization, by John Baez is short and pedagogical
Matthias Blau's primer on Geometric Quantization, one of the very few good primers (ps format only)

A. Echeverria-Enriquez, M. Munoz-Lecanda, N. Roman-Roy, Mathematical foundations of geometric quantization, arXiv: math-ph/9904008.

G. Sardanashvily, Geometric quantization of symplectic foliations, arXiv: math-ph/0110196.

Geometric quantization

See also

References

External links